SEO продвижение
А сейчас мы хотим обратиться к руководителям компаний и маркетинговых отделов. Основной целью, которую преследует профессиональное продвижение сайта, должно стать увеличение конверсии вашего ресурса, а следовательно, и увеличение количества ваших продаж. Поэтому, запомните: профессиональная компания, занимающаяся SEO-продвижением коммерческих проектов, с готовностью выполнит весь комплекс мероприятий, позволяющих не только увеличить посещаемость сайта, но и подвигнуть потенциального клиента на совершение целевого действия. При этом непрофессионалы, всего лишь, занимаются бездумным повышением позиций сайта в результатах поисковой выдаче. А без комплекса дополнительных мероприятий, такой подход никак не способствует увеличению конверсии.
Вывод прост: именно качество продвижения коммерческого проекта способно определить будущее всего вашего бизнеса. Следовательно, во всех случаях и при любых условиях вверять судьбу своего проекта следует только в руки настоящих профессионалов!
Как вы уже знаете, SEO – это целый комплекс мероприятий, направленных на повышение позиций интернет-ресурса в результатах поисковой выдачи. Следовательно, нашей основной задачей является привлечение максимального количества потенциальных клиентов — из поисковых систем на страницы вашего сайта. В своей деятельности мы используем множество проверенных приемов, объединенных в одну стратегию, разрабатываемую индивидуально для каждого продвигаемого проекта.
Если вас заинтересовало наше предложение, связаться с нами можно, используя контактные данные, представленные на сайте.
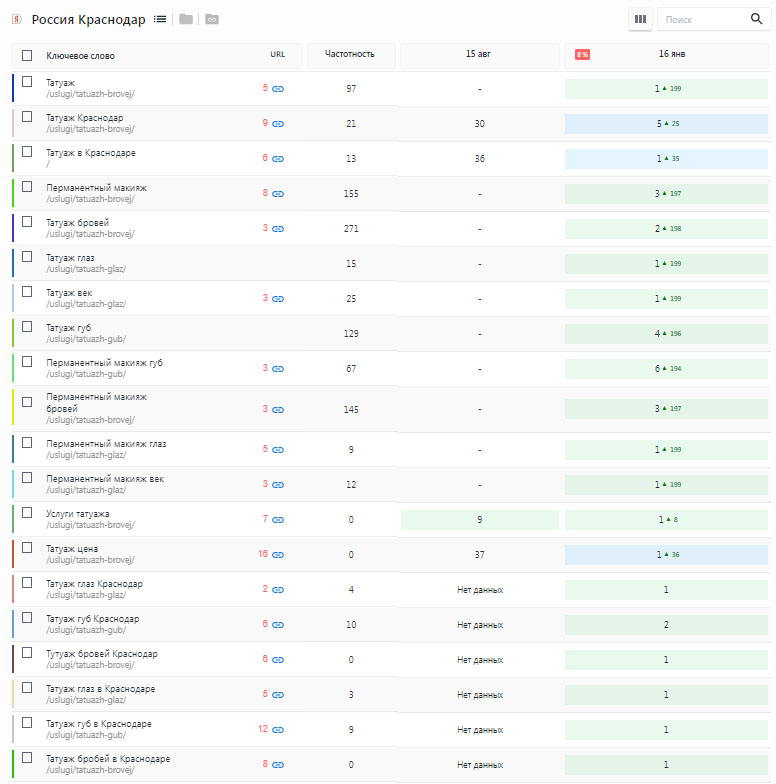
Пример SEO продвижение швейного производства
За год работы над проектом достигнуты результаты в топ 1-10 основных запросов, в том числе основные производственные запросы «Швейное производство»
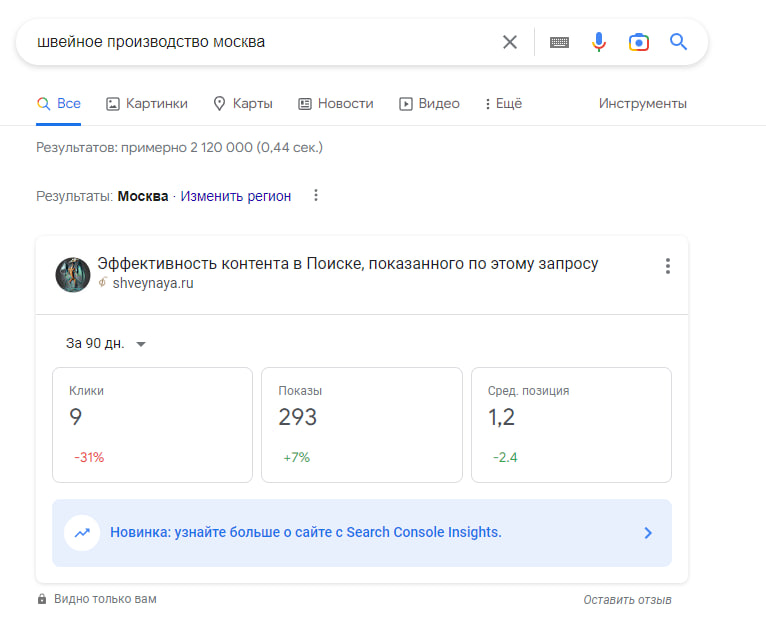
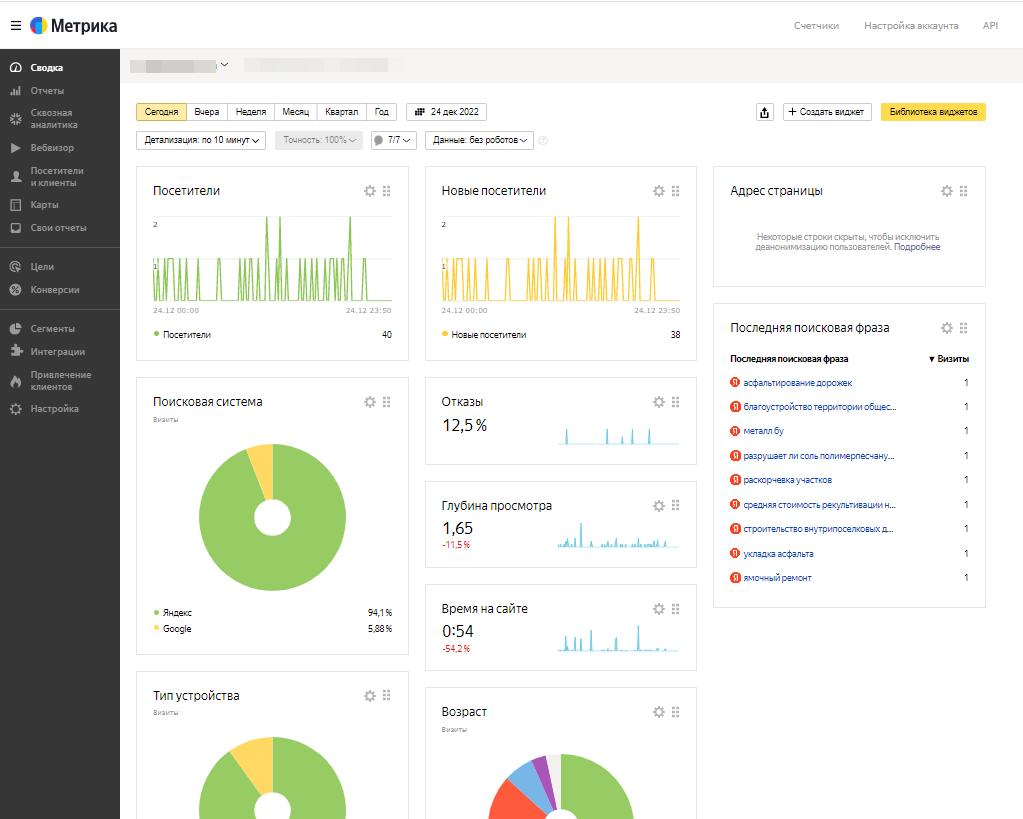
Взгляните на увеличение посещаемости ресурса
Инструменты разработчика позволяют отслеживать посещения и позиции Вашего сайта каждый день и взглянуть по-новому на продвижение.
Услуги SEO продвижения от частного специалиста
Интернет – самая интенсивная и прибыльная площадка для привлечения потенциальных клиентов к своим товарам и услугам.
Ежедневно миллионы пользователей используют просторы Интернета для поиска ответов на свои вопросы, а также для заказа и приобретения всевозможных товаров и услуг, в этом им помогают такие поисковые системы как Yandex, Google. Тысячи Ваших потенциальных клиентов ищут информацию о продукции, но находят не Вас, а Ваших конкурентов. Все эти потенциальные клиенты и покупатели заходят на сайт Ваших конкурентов и знакомятся с ИХ предложением, а не с Вашим. Чем интересны целевые пользователи? Они уже заинтересованы в покупке того или иного товара. Им не надо объяснять все преимущества использования товара, сравнивать технологии и вообще уговаривать использовать этот товар или услугу. Потенциальный клиент заинтересован, он приобретёт товар в любом случае, если не у Вас, то у Ваших конкурентов.
В ТОП уже через месяц!
Сайты услуг, производств, интернет-магазины и не только
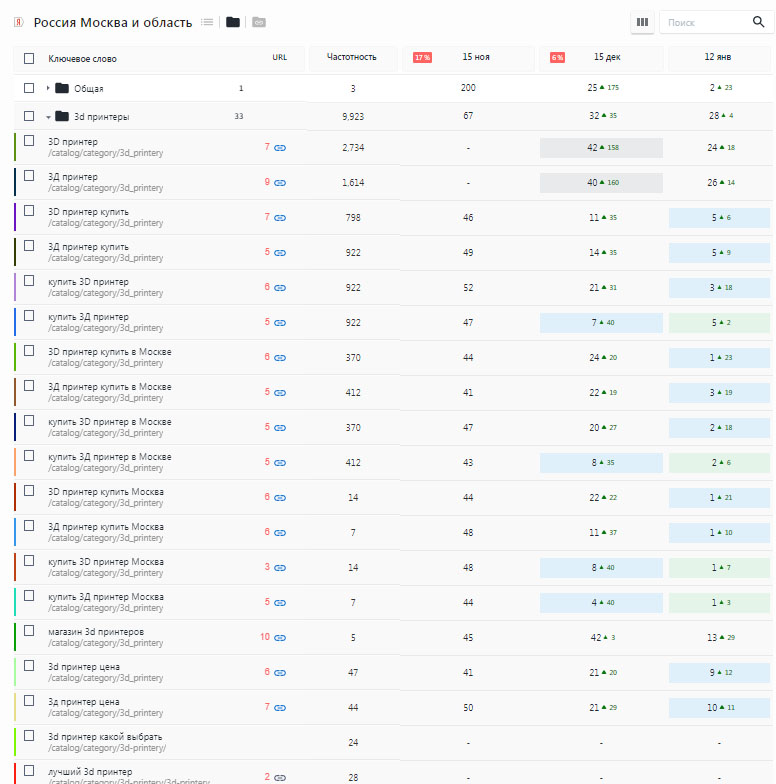
Как происходит вывод сайта в топ поисковых систем
Стоимость продвижения в 2 раза ниже чем у студий и агентств!
И работы выполнено в 5 раз больше!
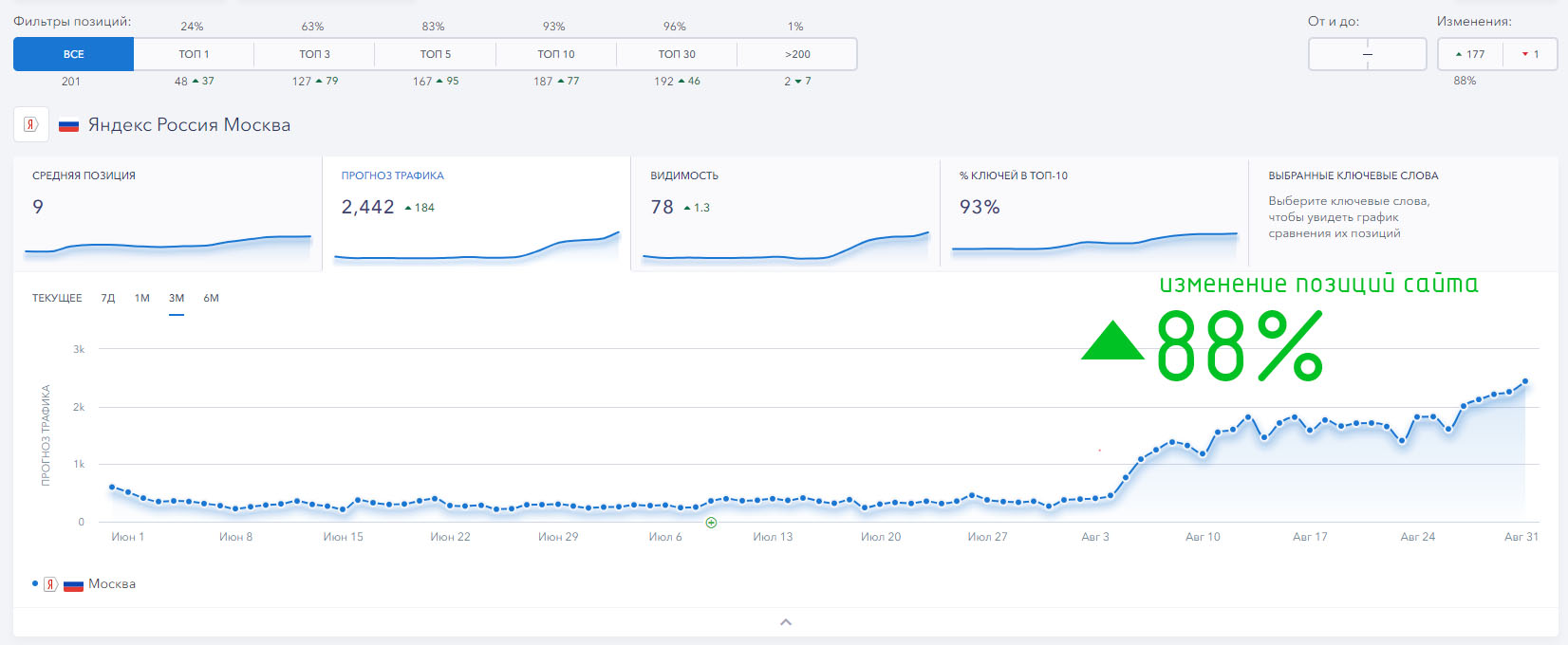
До топ 2 Москва
До топ 1-3
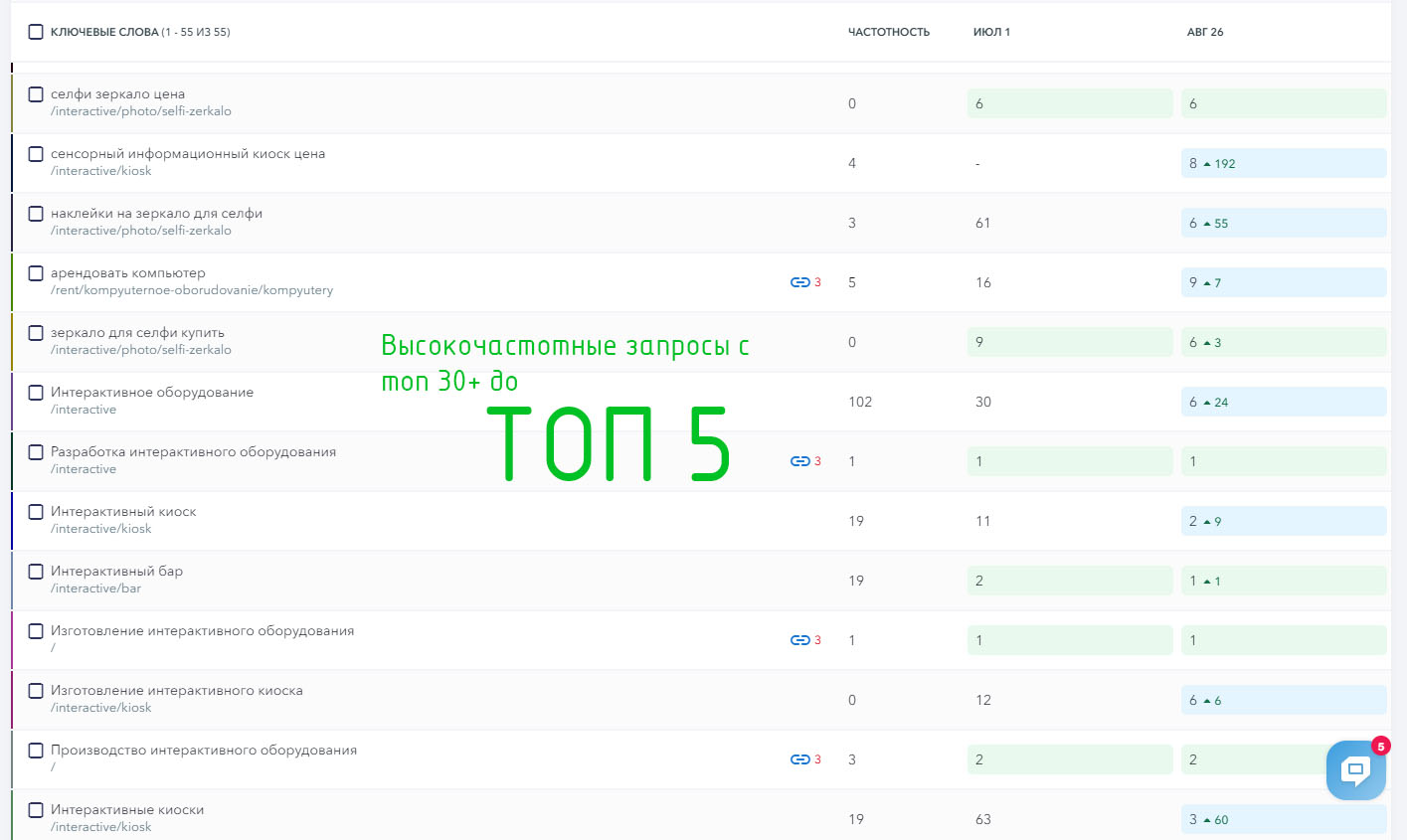
Сайт услуг
Выводим от 1 до 100 внутренних страниц в топ поисковых систем Яндекс и Google!
35000 рублей
Интернет-магазин
Вывел огромное множество кластеров и товаров. Высокочастотные и среднечастотные запросы в топ!
60000 рублей


Выберите нужное направление продвижения сайта
Продвигаем абсолютное большинство тематик, в том числе высококонкурентные
Очевидные преимущества частного SEO специалиста
Мои преимущества:
Агенства
- Очередной сотый проект
- Дополнительно выкачивают деньги
- Ничего не делают в итоге
Частный СЕО специалист
- Ваш проект у меня пятый
- Нет дополнительных трат и скрытых платежей
- Вывожу в ТОП уже спустя несколько недель продвижения
Продвижение сайта поможет решить Вам следующие вопросы:
- Поиск новых клиентов, партнёров, сотрудников.
- Продажа товаров или услуг.
- Информирование о своих конкурентных преимуществах и своей полезности.
- Обратная связь с потребителями своих услуг и товаров.
- Увеличение эффективности работы компании (сайта, отдельных бизнес-процессов)
- Формирование информационного поля и PR.
Продвижение сайтов включает в себя:
- анализ сайта заказчика
- анализ выдачи поисковых систем и конкурентов
- рекомендации по изменению внутренней структуры сайта
- рекомендации по изменению текстов, мета-тегов и тайтлов сайта
- составление семантического ядра (списка ключевых слов)
- работа с внутренними ссылками
- регистрация в рейтингах и каталогах
- покупка внешних ссылок
- составление отчетов по продвижению web-сайта
SEO продвижение с гарантией в договоре
При заключении договора на продвижение Вы можете получить сайт в подарок. Используйте эту возможность для раскрутки отдельных проектов или развития новых направлений деятельности. Мы поможем Вам грамотно спланировать рекламную кампанию. Сочетание поискового продвижения и контекстной рекламы позволит получать клиентов уже на следующий день. Наши клиенты платят только за результат. В течении месяца Ваш сайт приводит клиентов, а только в конце месяца вы оплачиваете результат. Сколько дней сайт находился в ТОП-10 — столько дней вы и оплачиваете. Разнообразный и богатый опыт постоянный количественный рост и сфера нашей активности требуют от нас анализа позиций. После того как вы определились с тарифами по продвижению, мы окончательно согласуем и фиксируем условия взаимовыгодного сотрудничества и оформляем договор. Каждый из методов раскрутки сайтов позволяет направить на сайт клиента именно тех пользователей, которые уже готовы приобрести товар или заказать услугу.
Сотрудничество с нами позволит Вам значительно увеличить прибыль и оставить конкурентов позади.
Заставьте Ваш сайт работать и приносить клиентов! Интернет-сайт – это продавец-консультант, менеджер по продажам, диспетчер, менеджер по работе с клиентами, который работает круглосуточно, без выходных и не требует повышения зарплаты.
Вы получаете детальный план работ
Мы предоставляем вам план проекта
на текущий месяц с подробным описанием
работ и сроков. По завершению месяца
вы получаете детальный отчет.
Вы защищены гарантиями в договоре
Все наши договоренности и принятые
обязательства по KPI фиксируются в
договоре и SLA, которые исключают,
скрытые платежи или любые другие
невыгодные для вас условия.
Вы работаете с напрямую со специалистом
Основообразующими сотрудниками
в нашей команде являются технические
эксперты и опытные специалисты по
работе с клиентами, которые всегда
на связи.
Вы получаете супер быстрый результат
В нашей компании все сотрудники работают
в штате и максимально замотивированы на
достижение результата. Это позволяет нам
четко в срок выполнять поставленные
задачи.
Стоимость SEO продвижения разных сайтов
Что мы можем вам предложить?
Реклама в интернете методами донесения информации до потребителя очень сильно отличается от классической. Ведь интернет позволяет собирать данные о пользователях, понимать что им лучше и анализировать не только рынок, но и интересы покупателей. Именно поэтому реклама в интернете требует не только творческого подхода, но и технического.
Наши сотрудники могут составить для вас любой слоган, разработать дизайн объявления, подготовить презентацию товара или услуги. Но, что более важно, мы готовы донести эту рекламу до тех пользователей интернета, которым будет действительно интересно ваше предложение. Так что целевая реклама в сети – наш конёк.
Так же мы можем помочь вам продвинуть уже готовый бренд, который по каким – то причинам в сети не замечают. Наши специалисты по рекламе проанализируют ваш проект и помогут направить его в нужное русло, а SEO – специалисты помогут продвинуть ваш сайт. Так что наше рекламное агентство сможет стать надежным партнером вашего бизнеса.
Почему стоит обратиться к нам?
Наше главное преимущество – всесторонний подход к рекламе. Сотрудники нашего рекламного агентства даже к самой простой задачей разбираются крайне тщательно, применяя как творческий подход, так и знания в сфере информационных технологий.
Кроме того, большое количество специалистов может полностью самостоятельно не только создать действенную и интересную рекламу, но и рассказать его целевой аудитории через сайты, поисковые системы, соцсети. Так что ваша реклама будет видна только заинтересованному кругу клиентов, что сократит расходы и увеличит продажи.
Самым значимым нашим преимуществом можно назвать сочетание богатого опыта и индивидуального подхода. Перед началом работы наше рекламное агентство всегда тщательно изучает материалы и интересуется пожеланиями клиентов, после чего работа поручается тому специалисту, который уже имеет опыт работы в нужной сфере. Это не только увеличивает скорость работы, но и значительно повышает её качество.